2. L'ottica marginalista-neoclassica, con particolare riferimento
ad alcuni contributi teorici recenti
Con l'avvento di quella che in seguito sarebbe stata denominata "Rivoluzione marginalista", gli economisti
costruiscono le loro teorie sul concetto della massimizzazione dell'utilita' attraverso lo scambio, in un mercato
dove il concetto di scarsita' viene esteso a tutti i fattori produttivi: terra, lavoro e capitale. Tale concetto
di scarsita' e' essenzialmente relativo, cioe' si basa sulla disponibilita' nei confronti dei desideri in un determinato
istante.
E' ovvio che, se il marginalismo sviluppa la sua teoria a partire da un concetto di "scarsita' statica",
il problema dell'esauribilita' delle risorse naturali perde la sua rilevanza. Infatti quel che interessa e' semplicemente
indagare come in un contesto statico la produzione sia vincolata dalla scarsita' (e non solo di risorse naturali)
e studiare il funzionamento del mercato, per individuare le condizioni che assicurano l'ottima allocazione delle
risorse stesse.
Quindi le tematiche affrontate dai marginalisti sono ben diverse da quelle dei classici e portano a non considerare
piu' come centrali i problemi relativi al processo di crescita dell'economia: "alla base della costruzione
marginalistica e' la nozione di risorse scarse di cui si vuole studiare l'impiego razionale in vista di fini riferiti
a un preciso momento di tempo; l'analisi classica studia invece le implicazioni che ha l'espansione delle
risorse disponibili"(18).
Queste brevi considerazioni dovrebbero aver sottolineato adeguatamente la causa principale del disinteresse dei
marginalisti verso il problema dell'esauribilita' delle risorse naturali. Quest'ultime vengono talvolta prese in
considerazione solamente per definirle quale "capitale naturale", ma comunque "non deperibile"(19),
o per studiare il modo in cui vengono a determinarsi la rendita e i prezzi a loro relativi.
E' possibile individuare altre ragioni alle quali, probabilmente, si puo' ricollegare il disinteresse dei neoclassici
verso tali problematiche.
Innanzitutto bisogna ricordare che, nell'analisi marginalistica gli operatori economici agiscono sulla base di
un calcolo razionale, in modo di massimizzare le loro funzioni obiettivo (in genere la funzione dell'utilita' e
quella del profitto). E' questa comunque una razionalita' di breve periodo, poiche' ben difficilmente il singolo
individuo potra' considerare nei propri obiettivi questioni sociali (che tuttavia lo investono e possono diminuire
il suo benessere) e tantomeno di giustizia inter-generazionale, quale l'eventuale necessita' di conservare delle
risorse per i posteri. Al limite, se lo facesse, in quest'ottica cio' che interessa all'economista consiste solamente
nel fatto che e' cambiata la sua funzione di utilita'.
Nella ricerca delle forme razionali dell'attivita' economica e delle strutture che garantiscono l'ottima allocazione
delle risorse scarse, i marginalisti hanno rivendicato una certa "generalita' ed asetticita'" della loro
scienza (20), comparandola alla ricerca delle leggi fisiche e meccaniche, e quindi utilizzando strumenti assai
simili nell'analisi dei fenomeni economici. In quest'ottica, come sottolinea Zamagni (21), le leggi economiche
vengono ad assumere un carattere universale, valido in qualsiasi contesto, ed e' quindi necessario escludere dallo
studio dell'economia le relazioni sociali.
Lo stesso autore evidenzia come questa possa essere considerata una reazione alle teorie di Marx, ma piu' in generale
a quelle di tutti i classici, che fecero uso di termini e concetti che presupponevano una suddivisione in classi
e sulle teorie dei quali Marx sviluppo' le sue idee "pericolose e sconcertanti".
In un clima di profondo conflitto sociale e di critica al sistema capitalistico le idee marginalistiche avrebbero
quindi stornato totalmente l'attenzione da "vecchi problemi indesiderabili".
E' cosi' che nella teoria neoclassica puo' emergere un'apologia del mercato perfettamente concorrenziale, pretesa
non tanto quale difesa degli interessi di una certa classe, ma quale risultato di una ricerca scientifica obiettiva:
"si tratta di dimostrare che l'economia capitalistica realizza un tipo di organizzazione sociale che e' prossimo
all'ideale, e cio' nel senso che le regole del mercato consentono di raggiungere una situazione in cui l'armonia
degli interessi tra gli individui e la mas-simizzazione degli obiettivi che ciascuno si prefigge di raggiungere
configurano un ottimo sociale."(22)
Parallelamente a queste considerazioni si puo' quindi sottolineare che tra gli aspetti "indesiderabili"
delle teorie classiche, oltre a quelli tipicamente "marxisti" relativi ai conflitti sociali, si potrebbero
annoverare anche quelli, tipicamente "malthusiani", dei limiti allo sviluppo economico causati dalla
scarsita' assoluta delle risorse naturali.
Infine bisogna anche ricordare che per i neoclassici biso-gna dedicarsi all'economia politica come ci si dedichereb-be
all'acustica o alla meccanica. Quindi se le leggi della fisica hanno influenzato gran parte della scienza economica,
probabilmente si e' tralasciato un possibile approc-cio "biologico", forse piu' appropriato per comprendere
le conseguenze di uno sviluppo economico in un ambiente con risorse naturali scarse.
Piu' in generale si puo' osservare come questo atteg-giamento di disinteresse verso il problema dell'esauri-bilita'
delle risorse abbia riguardato la maggior parte degli economisti dopo i classici, compresi quelli non propriamente
appartenenti alla scuola neoclassica, perlomeno fino ai nostri tempi.
Tra i fondatori della scuola marginalista, per quello che riguarda l'analisi dei problemi relativi alle risorse
naturali, fa comunque eccezione Stanley Jevons che, nel suo famoso saggio "The coal question" del 1865,
affronto' il problema del rapido esaurimento del carbone in Inghilterra.
Sebbene le sue previsioni si dimostrassero errate (grazie specialmente al progresso tecnico che avrebbe consentito
la sostituzione del carbone con altre fonti energetiche), la sua opera deve essere considerata come "un primo
serio sforzo tendente ad analizzare lo sviluppo economico di un paese in relazione ai limiti imposti dalla scarsita'
delle sue risorse energetiche". (23)
Dopo Jevons, a parte qualche rara eccezione, bisogna attendere tempi piu' recenti perche' si affrontino i problemi
posti dall'esauribilita' delle risorse naturali.
Gia' negli anni sessanta si sentono le prime voci preoccupate per l'inquinamento, i danni ambientali e tutti i
diversi "costi dello sviluppo" causati dalla crescente industrializzazione.
In particolar modo dopo la crisi petrolifera degli anni settanta nasce un dibattito vivace, che ha stimolato anche
alcuni economisti a riscoprire interesse per questo argomento.
Sebbene altre scuole moderne hanno approfondito (24) o avrebbero potuto approfondire, dal loro punto di vista,
il problema delle risorse esauribili, in questo campo il dibattito sul piano puramente teorico sembra sia stato
quasi interamente "monopolizzato" da una serie di studi sviluppati nell'ambito di alcuni filoni della
scuola neoclassica. E' quindi opportuno analizzare questi lavori, anche perche' probabilmente sono i soli contributi
della teoria economica che siano stati usati per dare una risposta alle voci preoccupate per l'esaurimento delle
risorse naturali, entrando a pieno titolo nella discussione in corso non solo a livello accademico.
In particolare sono stati utilizzati per criticare "l'allarmismo" provocato dai movimenti ecologisti
e dai lavori di alcuni studiosi, tra i quali in particolare il famoso rapporto del M.I.T. al Club di Roma, The
Limits to Growth (25).
A proposito di queste teorie economiche, prima di illustrarle e' opportuno sottolineare che, mentre la maggior
parte degli economisti, al di la' delle diverse prese di posizione, sono intervenuti nel dibattito conoscendone
le basi teoriche e le ipotesi fondamentali e quindi, se vogliamo, i pregi e i limiti (26), a livello politico sono
state talvolta invocate per affermare come il problema delle risorse naturali viene automaticamente risolto dall'esistenza
di un libero mercato concorrenziale. Piu' in generale si puo' dire che, a livello "giornalistico", ad
un certo "catastrofismo" originato da una lettura acritica delle tesi del M.I.T., si e' contrapposta
(anche senza conoscere queste nuove teorie) la fiducia "cieca" nel mercato che discende da un'accettazione
superficiale della teoria neoclassica "tradizionale", sostenendo che le forze della domanda e dell'of-ferta
assicurano l'efficientemente utilizzazione delle risorse nel tempo.
Hanno scritto a proposito Dasgupta ed Heal (27) come chi fa quest'ultima affermazione sia spesso totalmente ignaro
di cio' che significa, oppure nel migliore dei casi non conosca le condizioni sotto le quali puo' essere difesa.
Coloro che hanno una grande fede nel meccanismo del mercato sarebbero sorpresi, aggiungono, se fossero eruditi
sulle caratteristiche che devono essere stabilite perche' questa fede sia giustificata. Tuttavia gli stessi autori
sostengono l'utilita' di questi studi, perche' spesso ci permettono di individuare i difetti nell'allocazione delle
risorse quando si riconosca che alcune ipotesi fondamentali del modello sono violate nel mondo reale.
Queste teorie riprendono e approfondiscono alcune analisi neoclassiche dei problemi relativi alle risorse naturali,
gia' anticipate da qualche economista anche molto prima degli anni settanta, a partire dall'articolo di Harold
Hotelling pubblicato nel 1931 sul Journal of Political Economy (28).
La maggior parte di questi lavori impiegano prevalente-mente gli stessi strumenti matematici (la teoria del controllo
ottimale) e affrontano problematiche molto simili.
Non e' possibile esporre in queste pagine i singoli contributi di tutti gli autori che si sono cimentati su tale
argomento; sembra piu' opportuno cercare di illustrarne per sommi capi le analisi e le conclusioni, senza neppure
soffermarsi su tutte le numerose e talvolta complesse dimostrazioni matematiche.
Innanzitutto bisogna cercare di individuare i vari "filoni" di ricerca in relazione alle particolari
problematiche di volta in volta affrontate.
In generale questi studi si suddividono tra quelli dedicati alle risorse non rinnovabili (esauribili) e quelli
concernenti le risorse rinnovabili.
Alcuni autori si propongono di determinare l'andamento del prezzo di una risorsa, effettuando diverse ipotesi sui
regimi di mercato e su altre variabili; da queste ricerche, ovviamente, e' possibile dedurre le differenti implicazioni
per la conservazione delle risorse naturali, relative alle varie ipotesi. In questi studi, come vedremo, si parte
dal presupposto che, dato un certo tasso di interesse determinatosi sul mercato, il proprietario delle risorse
cerchi di massimizzare il valore attuale dei profitti futuri; cioe' si determina un tasso di sfruttamento ottimo
da un punto di vista privato. Si cerchera' nei paragrafi 2.1 e 2.2 di illustrare questi modelli in relazione alle
risorse non rinnovabili (esauribili) e a quelle rinnovabili.
Altri autori si sono posti la domanda se il tasso di sfruttamento determinato dal mercato non potrebbe eccedere
quello desiderato o desiderabile socialmente. Al di la' dei notevoli problemi posti dalla necessita' di definire
un criterio accettabile di misurazione del "benessere sociale", questo ha portato all'elaborazione di
alcuni studi, nell'ambito della teoria dello sviluppo economico ottimale, dove ci si propone di determinare il
tasso di sfruttamento ottimo delle risorse da un punto di vista sociale. Nel paragrafo 2.3 si cerchera' di illustrare
alcuni sviluppi e problemi relativi a questo nuovo approccio alla teoria dello sviluppo economico ottimale (29).
2.1. Il prezzo di una risorsa esauribile in regime di concorrenza
perfetta e in regime di monopolio.
Cerchiamo ora di vedere l'impostazione e i possibili sviluppi di un modello relativo all'ottimo impiego delle risorse
naturali.
La caratteristica dell'esauribilita' delle risorse impone di adottare una prospettiva di lungo periodo in relazione
al fatto che esse devono essere impiegate in modo ottimo fino al momento in cui le riserve non siano completamente
esaurite.
Gli studi come quello che andiamo a descrivere ricorrono ai tradizionali concetti dell'analisi neoclassica, utilizzando
il prezzo come indice di scarsita' e come valore d'equilibrio tra domanda e offerta di lungo periodo.
Generalmente l'analisi e' condotta con riferimento a modelli d'equilibrio parziale, vale a dire quelli riguar-danti
singoli mercati. Viene posta l'ipotesi dell'esistenza di mercati a termine, ove sia possibile acquistare o vendere
la proprieta' delle risorse naturali in qualsiasi periodo di tempo. Come sottolineato dalla Targetti Lenti (30),
si tratta evidentemente di una ipotesi molto "forte" di rilevanza puramente teorica.
Questo modello si basa sull'ipotesi che i proprietari considerino l'impiego di queste risorse al pari di quello
di qualsiasi altro bene capitale che produce reddito nel tempo. La condizione di equilibrio e' quella per cui in
ogni istante di tempo il proprietario di un giacimento manifesta indifferenza tra lasciare la risorsa nel suolo
o estrarla, per il fatto che il valore del giacimento cresce in base ad un saggio pari a quello di interesse.
In un regime di concorrenza perfetta si suppone l'esistenza di piu' imprese che controllano una riserva ciascuna.
Siano qt e pt, rispettivamente
il prezzo di un'unita' di risorsa estratta e il prezzo di un'unita' di risorsa non estratta, al tempo t.
In assenza di costi di estrazione, in una situazione di equilibrio pt deve quindi crescere ad un saggio uguale
al tasso di interesse r. Cioe' la funzione del prezzo di un'unita' di risorsa non estratta e':
pt = poert
Per determinare la funzione del prezzo qt di un'unita' di risorsa estratta bisogna ipotizzare
una funzione di costo di estrazione. Sia R il tasso di estrazione ed S la quantita' di risorsa disponibile. Si
puo' definire una funzione di costo di estrazione del tipo :
C = f(R,S,t) dove fR'>0, fS'<0,
ft'<0.
Questo significa che C dipende direttamente dal tasso di estrazione e inversamente dalla quantita' disponibile;
inoltre con il passare del tempo nuove tecnologie possono abbassarlo.
Rimandiamo, per ora, la questione del progresso tecnologico, scegliendo quindi una funzione piu' semplice:
C = f(R,S).
Il prezzo qt risulta:
qt = pt + dC/dRt (a1)
cioe' e' uguale alla somma tra il prezzo di un'unita' di risorsa non estratta e il costo marginale di estrazione.
Come e' noto, la condizione di ottimo in un mercato concorrenziale e' data dall'uguaglianza tra il prezzo e il
costo marginale di produzione. Qui' al costo marginale si aggiunge pt,
che e' definito come "un costo opportunita' dato dal beneficio ottenuto dall'utilizzazione della risorsa nel
periodo attuale piuttosto che in un tempo futuro"(31) oppure come una "rendita di scarsita'".
La relazione (a1) viene trovata supponendo che ogni proprietario agisca in modo da massimizzare il valore attuale
dei profitti ottenibili dallo sfruttamento della risorsa.
Quindi il problema puo' essere cosi' impostato:
massimizzare
![]() [ qtRt - C(Rt,St) ] e-rtdt
[ qtRt - C(Rt,St) ] e-rtdt
sotto i vincoli: dSt/dt
= -Rt
e So = So
In questo modo oltre alla (a1) si trova la funzione che ci indica come varia pt nel tempo:
dpt/dt = rut + dC(Rt , St) /dSt (32).
In seguito e' possibile fare varie ipotesi sui costi marginali di estrazione, supponendoli costanti o variabili
relativamente ad St.
Nel caso di costi marginali di estrazione costanti si nota come, con il passare del tempo, il costo di estrazione
diventa trascurabile e il prezzo della unita' di risorsa estratta e' dato essenzialmente dal prezzo della unita'
di risorsa non estratta, che cresce al saggio r.
Se esiste un sostituto il prezzo della risorsa non puo' salire indefinitivamente, ma ha un limite dato dal prezzo
del sostituto, che puo' essere un bene producibile o un'altra risorsa (con un costo marginale di produzione o di
estrazione piu'alto di quello di estrazione della prima).
In questo contesto il prezzo della risorsa cresce fino a quando essa si sara' esaurita; in quel momento, a partire
dall'ultimo prezzo della risorsa scomparsa, diventa economico il sostituto.
Conoscendo l'entita' delle risorse e i costi di estrazione o produzione e' possibile calcolare il tempo T, quando
la prima risorsa sara' esaurita e il sostituto sara' messo in vendita.
Quello che si e' appena detto nel caso dell'esistenza di un sostituto, vale anche quando ci sono giacimenti della
stessa risorsa, ma di diverso tenore e con diversi costi di sfruttamento.
In realta' raramente l'andamento del prezzo di una risorsa esauribile
puo' essere studiato in condizioni di certezza, perche' molte variabili sopra accennate possono essere incerte
e quindi vanno considerate come variabili casuali.
L'incertezza riguarda:
1) L'entita' delle riserve, di cui generalmente si hanno solo delle stime, che possono essere modificate da attivita'
di esplorazione e di ricerca.
2) Le possibilita' di sostituzione.
Rispetto all'entita' delle riserve si sono costruiti dei modelli basati sull'ipotesi che il ritrovamento di nuove
riserve diminuisca il costo di estrazione.
Sia R* il tasso di ritrovamento di nuove riserve e C2(R*) il costo
dell'attivita' di esplorazione.
I proprietari della risorsa cercherebbero di massimizzare:
![]() [ qtRt - C1(Rt,St) - C2(R*) ] e-rt dt
[ qtRt - C1(Rt,St) - C2(R*) ] e-rt dt
Sotto il vincolo dS/dt = Rt*
- Rt.
Si trova cosi' un livello ottimo di esplorazione e si nota come, in genere, il prezzo cresce piu' lentamente che
nel caso di produzione in assenza di esplorazione (a parte quando il costo marginale di estrazione e' costante).
Se si ipotizza che la scoperta di nuove risorse dipenda, oltre che dall'attivita' di esplorazione, dall'entita'
delle scoperte precedenti si conclude che, se inizialmente le riserve sono scarse, l'attivita' di esplorazione
viene subito iniziata ed e' possibile, come e' effettivamente accaduto per alcune risorse, che nella fase iniziale
dello sfruttamento il prezzo tenda a diminuire.
In un regime di monopolio l'imprenditore cerca anch'egli di massimizzare
il valore attuale dei profitti.
Poiche' in monopolio il prezzo dipende dalla quantita' prodotta cioe', nel nostro caso, da quella estratta, la
soluzione sara' diversa rispetto a quella in regime di concorrenza perfetta:
ut = (dqt/dRt)Rt + qt - dC(Rt,St)/dRt ,
e (dut/dt)/ut = r + [dC(Rt,St)]/ut
Si puo' osservare come il prezzo di un'unita' di risorsa non estratta ut e' uguale alla differenza tra ricavo marginale e costo marginale.
Per effettuare dei confronti con l'andamento del prezzo in regime di concorrenza, si effettuano le stesse ipotesi
sulla funzione di costo di sfruttamento.
Ipotizzando ricavi marginali decrescenti, domanda elastica e valore assoluto dell'elasticita' che aumenta al diminuire
del tasso di estrazione, e' possibile notare come in generale il prezzo cresce meno velocemente in regime di monopolio
piuttosto che in regime di concorrenza e quindi il prezzo iniziale in regime di monopolio risulta piu' elevato,
comportando una maggiore conservazione delle risorse.
In altri casi il prezzo in regime di monopolio potrebbe crescere ad un saggio superiore. Tuttavia la possibile
apparizione di sostituti rende improbabile una riduzione dell'elasticita' della domanda.
Se esiste un sostituto controllato dal monopolista, notiamo un aumento del tasso di sfruttamento e una riduzione
del prezzo della risorsa al di sotto del livello che possiamo rilevare in assenza del sostituto.
Se il sostituto e', come puo' accadere piu' spesso, producibile liberamente da altre imprese, il monopolista ha
convenienza a tenere inizialmente un prezzo piu' elevato (rispetto al caso non ci fosse un sostituto) per compensare
la riduzione che si avra' nel lungo periodo per la presenza di concorrenti: questo comporta quindi un tasso di
sfruttamento ancora minore.
In generale quindi un monopolista segue una politica maggiormente conservativa.
Da questa analisi si potrebbe dedurre che il problema di eventuali
limiti allo sviluppo economico, legati all'esaurimento fisico delle risorse, non si pone neppure.
Si puo' notare come, in generale, il prezzo di mercato della risorsa esauribile tende, nel lungo periodo, a crescere;
anche se, in un primo periodo, esso diminuisse per la progressiva riduzione dei costi di estrazione, la crescita
della "rendita di scarsita'" (il prezzo della risorsa non estratta) prima o poi compenserebbe questa
riduzione e il prezzo, in definitiva, continuerebbe a salire.
"Poiche' il prezzo di mercato e il tasso di estrazione sono connessi dalla curva di domanda della risorsa,
quando il prezzo di mercato sale, il tasso corrente di produzione scendera' lungo la curva di domanda. Presto o
tardi il prezzo di mercato sara' tanto alto da bloccare completamente la domanda. A quel momento la produzione
cadra' a zero. Se flussi e stock sono stati ben coordinati, attraverso il mercato o attraverso un ufficio del piano,
l'ultima tonnellata prodotta sara' anche l'ultima esistente nel terreno. La risorsa sara' esaurita nel momento
stesso in cui il suo prezzo diventera' talmente elevato da farla uscire dal mercato." (33)
Quindi la sparizione fisica della risorsa e' del tutto irrilevante per l'economista.
Questo ragionamento e' perfettamente coerente con la teoria analizzata. Se si e' sicuri dell'esistenza di un sostituto,
si e' gia' visto come il meccanismo di mercato dovrebbe far si' che questo diventi economicamente sfrut-tabile
nel momento stesso che la risorsa si esaurisce.
Altrimenti si puo' comunque prevedere l'apparizione futura di un sostituto, resa ancor piu' probabile dall'aumento
del prezzo della risorsa stessa, che dovrebbe incoraggiare investimenti crescenti nella ricerca di materiali alternativi.
In quest'ultimo caso pero' la data di apparizione del sostituto e' una variabile casuale.
Non e' stato messo abbastanza in rilievo, mi sembra, il probabile "shock economico", conseguente alla
brusca impennata del prezzo che si avrebbe all'avvicinarsi dell'esaurimento di una risorsa, quando ci si accorgesse
che, per la data prevista, in realta' non sara' possibile sostituirla. In questo caso le previsioni potrebbero
essere state troppo ottimistiche per la esagerata fiducia nei progressi della ricerca scientifica.
Nell'ipotesi, invece, che non si prevedessero sostituti, la pianificazione dello sfruttamento delle risorse dovrebbe
essere distribuita, teoricamente, in un periodo di tempo infinito.
Sembra comunque improbabile che un'impresa pianifichi la massimizzazione del valore attuale dei profitti in un
orizzonte temporale che vada oltre qualche decennio. In altre parole, l'ipotesi posta alla base del modello di
un comportamento razionale dell'imprenditore nel lungo periodo e' molto discutibile.
Oltre ai fattori che abbiamo gia' visto, ci sono molti altri dati di incertezza nell'analisi teorica illustrata,che
vanno dal fatto che nella realta' lo sfruttamento di risorse avviene in un regime di oligopolio (o comunque in
un regime intermedio tra i due studiati), a possibili eventi politici o tecnologici.
Ulteriori problemi sono dati dalle aspettative riguardo la rendita, quando non si verificano condizioni di equilibrio.
Se i proprietari della risorsa prevedono che il prezzo di mercato salira' in modo tale da far crescere la rendita
ad un saggio minore del tasso di interesse corrente, allora aumentano l'attuale sfruttamento (per poter investire
il ricavato in impieghi alternativi). Poiche' la produzione corrente e' aumentata il prezzo di mercato dovra' scendere
lungo la curva di domanda. Cosi' le aspettative pessimistiche portano a prezzi ancor piu' bassi e vengono ulteriormente
rinforzate. Considerazioni analoghe ma simmetriche valgono nel caso di aspettative riguardo la crescita della rendita
ad un saggio minore di quello corrente.
In entrambi i casi il disequilibrio iniziale si aggrava, e l'estrazione della risorsa si e' avviata verso un ecces-sivo
sfruttamento o verso un "razionamento speculativo". (34)
2.2. Lo sfruttamento ottimale di una risorsa rinnovabile
Per analizzare i problemi relativi alle risorse rinnovabili bisogna conoscere le leggi di crescita che
ne determinano la quantita' esistente in un dato momento.
L'esempio tipico e' quello della crescita di una popolazione animale o vegetale, data dal saldo tra individui nati
e morti. I tassi di natalita' e mortalita' dipendono da numerosi fattori, tra cui la dimensione della specie, le
sue caratteristiche biologiche, la disponi-bilita' di alimenti, l'esistenza di altre specie, ecc.
Indicando con X la dimensione della specie, e' possibile esprimere una legge di crescita con una funzione differenziale
del tipo : dX/dt = f(X).
Una funzione della crescita piuttosto generale e' quella logistica sviluppata da Alfred Lotka e molto utilizzata
negli studi economici sulle risorse rinnovabili.
Tale legge presume che:
1) Esiste un livello di minima popolazione vitale X , tale che popolazioni inferiori sono destinate ad estinguersi;
2) Al di sopra del livello minimo la popolazione si riproduce a tassi crescenti fino ad una dimensione X*;
3) Oltre X* le condizioni ambientali sono meno favorevoli, a causa dell'aumento della popolazione, e quindi essa
si riproduce a tassi decrescenti;
4) Esiste un livello di massima popolazione che l'ambiente puo' sostenere dato da ![]() , dove la crescita cessa del tutto.
, dove la crescita cessa del tutto.
Nella figura 1 e' rappresentata una funzione con tali caratteristiche. Si noti che la dimensione a cui la risorsa
tende dipende dalla dimensione iniziale Xo:
1) per Xo < X la popolazione decresce e si estingue,
2) per Xo = X la popolazione e' stazionaria,
3) per X < Xo <= X* la popolazione aumenta a tassi crescenti,
4) per X* < Xo < X la popolazione aumenta a tassi decrescenti,
5) per Xo = ![]() la popolazione
e' stazionaria
la popolazione
e' stazionaria
6) per Xo > ![]() la popolazione
decresce e torna alla dimensione X
la popolazione
decresce e torna alla dimensione X
Figura 1 : Funzione logistica
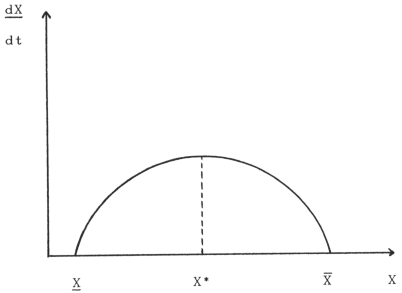
Al punto X* (dove df(X)/dX = 0) abbiamo un punto di massimo, cioe'
il tasso di rigenerazione e' il piu' alto possibile.
Nello studio dello sfruttamento ottimo interessano quelle risorse con X > X, perche' altrimenti la risorsa
sarebbe destinata ad estinguersi, di per se' nel caso di X < X e non appena si iniziasse lo sfruttamento
nel caso di X = X.
Se indichiamo con Yt il tasso di sfruttamento al tempo t, la legge
di crescita ne risulta cosi' modificata:
dX/dt = f(Xt) - Yt.
Se si suppone l'esistenza di condizioni di concorrenza perfetta il prezzo della risorsa e' dato e indipendente
dal tasso di sfruttamento.
Il comportamento delle imprese comunque e' diverso a seconda che le risorse siano di proprieta' privata oppure
di proprieta' comune.
Nel primo caso l'obiettivo di massimizzare i profitti e' raggiunto attraverso decisioni sia sulla quantita' di
risorsa da conservare sia sul tasso di sfruttamento.
Nel secondo caso piu' di una impresa ha diritto ad appropriarsi della risorsa e puo' decidere solo il proprio tasso
di sfruttamento.
Il caso di proprieta' privata della risorsa puo' essere cosi' formalizzato:
rendere massimo
![]() [qtYt - C(Yt,Xt)] e-rt dt (b1)
[qtYt - C(Yt,Xt)] e-rt dt (b1)
sotto il vincolo dX/dt = f(Xt)
- Yt
dove, se C(Yt,Xt) e' il costo dello sfruttamento e qt il prezzo di mercato
della risorsa, la (b1) rappresenta il valore attuale dei profitti ottenibili.
La soluzione e' data da:
qt = ut + dC(Yt,Xt)/dYt (b2)
dut/dt = rut - ut df(Xt)/dXt + dC(Yt,Xt)/dXt .
La prima relazione ci mostra che, come nel caso delle risorse non rinnovabili, il prezzo della risorsa e' dato
dal costo marginale di sfruttamento e dalla rendita.
La variazione della rendita nel tempo e' differente da quella trovata per le risorse non rinnovabili, perche' dipende
anche da ut df(Xt)/dXt. Quest'ultimo addendo e' dovuto al fatto che una risorsa esauribile puo' rigenerarsi
naturalmente.
Per determinare il tasso di sfruttamento ottimo, bisogna effettuare delle ipotesi sulla funzione di domanda della
risorsa e su quella del costo di sfruttamento. E' possibile comunque fare delle osservazioni di carattere generale.
Se il costo dello sfruttamento fosse piu' elevato del prezzo della risorsa, ovviamente il tasso ottimo di sfruttamento
sarebbe Yt=0.
Il caso che pone problemi di possibile estinzione della risorsa e' quello nel quale si determina un tasso Yt > f(Xt). Questa situazione si avvera
quando r e' relativamente elevato. In tal caso, infatti, il proprietario e' meno disposto a sacrificare i profitti
correnti per conservare la risorsa e, al limite, per tassi di interesse molto elevati non e' affatto interessato
alla conservazione (35).
Se pero' il costo dello sfruttamento e' crescente al diminuire della popolazione X, potrebbe accadere che, da un
certo punto in poi, i profitti si annullano e l'estinzione venga scongiurata.
Le possibilita' di estinzione dipendono, in ultima analisi, dalla relazione tra la dimensione minima vitale e la
popolazione minima a cui lo sfruttamento e' profittevole.
Tra questi due casi estremi vi e' quello nel quale un'im-presa ha convenienza a sfruttare la risorsa senza esaurirla.
In questo caso si considerano politiche di sfruttamento che mantengono inalterata la dimensione della specie, sfruttandola
ad un tasso uguale a quello di rigenerazione naturale (cioe' Yt=f(Xt)).
Data una certa popolazione iniziale Xo > X, un certo tasso
di interesse r e una certa funzione di costo dello sfruttamento, l'impreditore deve, per un certo periodo, sfruttare
la risorsa ad un tasso maggiore a quello di rigenerazione o, al contrario, non sfruttarla, per raggiungere una
dimensione ottimale.
Se dC(Yt,Xt)/dXt=0 ed r=0 la dimensione ottimale sarebbe X*, cioe' quella dove df(Xt)/dXt=0 e si ha il massimo tasso di
rigenerazione naturale. Ma poiche' solitamente dC(Yt,Xt)/dXt < 0 ed r>0 la dimensione
ottimale e' raramente quella ove si realizza questo massimo.
Nel caso di proprieta' comune della risorsa, l'impresa non puo' influire sulla sua conservazione e decide, per
massimizzare il profitto, di sfruttare la risorsa fino al punto in cui risulta
qt = dC(Yt,Xt)/dYt (b3)
cioe' dove il prezzo della risorsa e' uguale al costo marginale dello sfruttamento.
Questo caso puo' portare a significative diseconomie esterne nelle decisioni di sfruttamento, poiche'la risorsa
naturale contribuisce alla produzione ma non riceve alcun compenso.
La proprieta' comune della risorsa rende evidentemente molto piu' probabile un suo esaurimento, tuttavia anche
in questo caso il costo dello sfruttamento potrebbe diventare proibitivo prima dell'esaurimento della risorsa.
L'estinzione avviene quindi solo se si puo' ottenere un profitto dalla caccia dell'ultimo membro della popolazione.
"Storicamente lo sfruttamento di molte popolazioni biologiche ha seguito un modello caratteristico. Dapprima
una fase di sfruttamento, spesso abbastanza rapida e seguita da scoperte tecnologiche. Poi, con l'aumento dello
sfruttamento, vengono espressi timori per la sopravvivenza della popolazione e della relativa industria. Si adottano
quindi misure di conservazione, talvolta con successo, mentre in altri casi si e' agito troppo tardi e l'industria
crolla. In certi casi le specie sono state completamente sterminate o ridotte ad un livello al quale sono incapaci
di sopravvivere."(36)
Nasce quindi il problema di trovare delle politiche per evitare l'estinzione di alcune specie (sempre restando
nell'ottica di questa analisi "neo-classica").
Il criterio generale sara' quello di impedire lo sfruttamento della risorsa qualora la dimensione della specie
si avvicina a quella minima necessaria per la riproduzione.
Nel caso di risorse di proprieta' comune si dovrebbe intervenire per impedirne uno sovrasfruttamento in senso biologico.
Dapprima si proibisce lo sfruttamento per un certo periodo, fin a quando la specie ha raggiunto la dimensione ottimale,
per poi imporre una tassazione appropriata in modo che la risorsa non sia considerata un bene libero.
2.3. Il benessere sociale e lo sfruttamento ottimale di una
risorsa esauribile
Alcuni autori, come si e' detto, si propongono di determinare il saggio di sfruttamento ottimo per massimizzare
il benessere sociale.
Il problema principale nasce dal fatto che non esiste una definizione univoca del termine "benessere sociale".
Nella teoria della crescita economica ottimale, sviluppata da Ramsey ed altri economisti, si definisce questo concetto
come l'utilita' dovuta al consumo. Resta comunque aperto il problema della scelta di un'idonea funzione di utilita',
se teniamo conto del fatto che generalmente vengono scelte quelle che pongono meno problemi dal punto di vista
computazionale.
Secondo questa concezione utilitaristica il benessere sociale e' massimo quando e' massima la somma delle utilita',
dovute al consumo, di tutte le generazioni. Questo problema non sempre ha soluzione, a meno che non si ricorra
allo sconto delle utilita' delle generazioni future, rendendo convergente la somma delle utilita'. Lo sconto delle
utilita' e' stato duramente criticato da Ramsey per il fatto che da' meno peso alle generazioni future rispetto
a quelle presenti. Tuttavia alcuni autori ritengono tale sconto giustificato dall'incertezza riguardo le future
tecnologie; si pone in questo caso il problema della scelta del tasso da utilizzare, particolarmente delicata nel
caso in cui si considerino risorse esauribili.
Altri autori definiscono il benessere sociale in termini di consumo pro-capite.
R.M. Solow (37) ed altri economisti, ispirandosi alle regole di giustizia distributiva sostenute da Rawls (38),
hanno evidenziato come, per assicurare una certa equita' tra le diverse generazioni, il consumo pro-capite debba
essere costante nel tempo.
Mentre nella teoria utilitaristica c'e' la possibilita' che una perdita di utilita' per una generazione, sia piu'
che controbilanciata da un incremento per l'altra, questa concezione invece pone tutte le generazioni sullo stesso
piano.
Lo stesso Solow sottolinea comunque due importanti limiti di questo criterio. Innanzitutto e' necessario che vi
sia inizialmente uno stock di capitale sufficientemente elevato da garantire un certo benessere, altrimenti non
si farebbe che mantenere per sempre un basso livello di consumo. In secondo luogo, in caso di popolazione stazionaria
e progresso tecnico illimitato, lo definisce "stupidamente conservativo", dal momento che porta a consumare
lo stock di capitale per mantenere costante il consumo, quando questo potrebbe invece crescere esponenzialmente.
Ci sono altre definizioni di benessere, come quelle basate sulla rendita del consumatore o del produttore.
Nella teoria dello sviluppo ottimale, come noto, ci si propone la ricerca di traiettorie o sentieri temporali ottimali
per le variabili economiche. Il modello piu' usato, dovuto a Ramsey, e' quello ove si studia l'allocazione ottimale
del consumo aggregato Ct, data una certa funzione di produzione Y =
F(Kt) e a certe condizioni di investimento (cioe' di incremento del
capitale produttivo) date da dKt/dt = Y - C.
Nella teoria dello sfruttamento ottimale delle risorse esauribili si fa dipendere la funzione di produzione oltre
che da Kt (lo stock di capitale esistente al tempo t) anche da Rt (la quantita' di risorsa esauribile usata al tempo t): quindi Y = F(Kt, Rt).
Si e' visto che, secondo una concezione utilitaristica, il benessere sociale da massimizzare e' dato dalla somma
delle utilita' scontate di tutte le generazioni.
Data da U(Ct) l'utilita' dovuta al consumo Ct, il problema puo' essere cosi' formalizzato :
massimizzare
![]() e-dt U(Ct) dt
e-dt U(Ct) dt
sotto i vincoli: dK/dt = Y - C
![]() Rt dt <= So
Rt dt <= So
Kt, Ct, Rt >= 0
avendo indicato con d il tasso di preferenza inter-temporale e con So la quantita'
disponibile di risorsa esauribile.
E' evidente come, da un simile modello, si possono trarre diverse conclusioni, a seconda delle diverse ipotesi
formulate relativamente alle funzioni dell'utilita' e della produzione, e rispetto alla elasticita' di sostituzione
tra capitale e risorsa esauribile.
Dasgupta e Heal (39), hanno formulato una delle ipotesi tra le piu' note, studiando le condizioni di ottimalita'
nel caso che si prendano :
ipotesi 1 : una funzione di utilita' che sia, come usuale, monotonicamente crescente, strettamente concava e doppiamente
differenziabile ovunque, inoltre sia:
lim U'(C) = + ![]()
c-->o
e l'elasticita' dell'utilita' marginale
n(C) = - U''(C) C/U'(C)
| con + |
lim n(C) = n | > 0 |
| c-->o |
Ipotesi 2 : una funzione di produzione omogenea di primo grado, crescente, strettamente concava e derivabile.
Massimizzando
![]() e-dt U(Ct) dt
e-dt U(Ct) dt
con gli usuali vincoli e con Ko (>0) dato, l'Hamiltoniano
associato al problema si riduce a :
H = e-dt U(Ct) +e-dtpt ( F(Kt,Rt) - Ct ) - F Rt + e-dt mt Rt
con mt >=
0 e mtRt=0
e F > = 0 e F
(So - ![]() Rt dt) = 0
Rt dt) = 0
Le condizioni di ottimalita', come noto, sono le seguenti:
dH/dC = 0 (c1)
dH/dR = 0 (c2)
d(e-dtp)/dt = -dH/dK
(c3).
Dalla (c1) si ottiene : pt = U'(Ct) (c4);
dalla (c2) si ottiene : F = e-dt ( mt + pt dF/dRt ) (c5),
dalla (c3) si ottiene : d(e-dtp)/dt
= e-dtp dF/dK
(c6)
cioe' -(dp/dt)/p = dF/dK - d
(c7),
la (c7) e' la ben nota regola di Ramsey, che puo' essere cosi' riespressa :
(dC/dt)/C = (FK - d) / n(C) (c8)
da quest'ultima possiamo osservare come il sentiero ottimale del consumo e' influenzato, tra l'altro, dal tasso
di sconto intergenerazionale. Si e' gia' osservato come la scelta di un idoneo valore di d e' molto difficile e criticabile.
Se scriviamo FR=dF/dR ed FK=dF/dK,
quando Rt>0 lungo una traiettoria ottimale, qualora esista, la (c5)
diventa :
F = e-e-dt pt FR
(c9).
Perche' Rt sia maggiore di zero si suppone (Ipotesi 3):
1) Un'economia dove
lim FR = + ![]()
c-->o
cioe' il prodotto marginale della risorsa tende all'infinito quando il tasso di utilizzazione
tende a zero;
2) Oppure che la funzione di produzione sia tale per cui risulta F(K,0)=0, cioe' la produzione e' nulla in assenza
della risorsa.
In entrambi questi casi sara' Rt>0 per tutti i valori di t>0,
poiche' non converra' esaurire la risorsa in tempo finito.
Differenziando la (c9) rispetto al tempo possiamo ottenere la condizione :
(dFR/dt)/FR = -(dp/dt)/p
+ d (c10),
e usando l'equazione (c7) trasformarla in
(dFR/dt)/FR = FK (c11).
La condizione (c11) indica che lungo una traiettoria ottima, che soddisfi le tre ipotesi avanzate, la variazione
della produttivita' marginale della risorsa esauribile deve eguagliare la produttivita' marginale del capitale.
Dasgupta e Heal dimostrano quindi che:
1) lungo una traiettoria ottima, qualora esista, un intervallo durante il quale R=0 non puo' essere seguito da
un intervallo nel quale R>0;
2) lungo una traiettoria ottima, qualora esista, Rt e' una funzione
continua di t.
Inoltre, o Rt>0 per tutti i valori di t>=0, oppure esiste un
tempo T>0 tale che Rt>0 per 0<=t<T ed Rt=0 per t>=T.
Vediamo cioe' come, nel caso che non si realizzi una delle condizioni dell'ipotesi 3, la risorsa puo' essere esaurita
in un tempo finito.
L'opportunita' di esaurire una risorsa dipende anche dall'elasticita' di sostituzione tra capitale e risorsa esuribile.
Tale elasticita' dipende dalla funzione di produzione ed e':
E = [d(K/R)/d(FR/FK)] [(FR/FK)/(K/R)] (c12).
Se risulta E>1 la risorsa e' inessenziale in quanto e' possibile ottenere una produzione positiva anche in assenza
di utilizzazione della risorsa. Probabilmente essa sara' esaurita abbastanza velocemente in modo da sostenere il
consumo e contemporaneamente accumulare uno stock di capitale che permetta poi di mantenerlo.
Quando E<1 la produzione che si puo' ottenere nel sistema economico e' limitata. In assenza di progresso tecnico
non sarebbe quindi possibile mantenere indefinitivamente qualunque consumo pro-capite.
Se E=1 la funzione di produzione e' di tipo Cobb-Douglas e rappresenta un caso limite tra gli altri due.
In generale in una traiettoria ottima, tanto maggiore e' tale elasticita' e tanto piu' deve aumentare la quantita'
di capitale in rapporto alla quantita' di risorsa utilizzata.
Molti autori, trattando il problema, studiano il caso in cui E<=1 perche' e' questo quello in cui la presenza
di risorse esauribili influisce sulla possibilita' di crescita.
Analizzando diverse funzioni che abbiano le proprieta' evidenziate e' possibile studiare le caratteristiche di
una traiettoria ottima.
In generale, comunque, si puo' concludere che gioca un ruolo importante il tasso di preferenza intertemporale in
relazione all'elasticita' E.
Un'analisi cosi' impostata e conclusa ha comunque numerosi limiti:
1) E' un modello unisettoriale in cui l'unico bene prodotto puo' essere consumato ed accumulato.
2) Il benessere sociale e' scontato al tasso ë; criterio, come gia' osservato, molto contestato.
3) Presuppone la conoscenza della quantita' totale di risorsa disponibile.
4) Non si e' considerata la dinamica della popolazione.
5) Si e' supposta l'assenza di progresso tecnico.
6) Si e' trascurata la possibilita' di sostituzione della risorsa (a parte quella con il capitale).
Alcune di queste considerazioni vengono comunque riprese in molti studi e il modello viene quindi ulteriormente
complicato.
Solow (40) e altri autori, come gia' osservato, preferiscono un'altra concezione di benessere per la quale il consumo
pro-capite deve essere costante nel tempo.
Egli ha dimostrato, usando una funzione di produzione del tipo Cobb-Douglas che, in assenza di progresso tecnico
e con popolazione costante, se l'elasticita' della produ-zione rispetto al capitale e' maggiore di quella rispetto
alla risorsa esauribile, e' possibile mantenere un certo consumo pro-capite indefinitivamente. Solow cita a propo-sito
l'esistenza di alcuni calcoli, fatti da W.Nordhaus e J.Tobin (41), i quali suggerirebbero che l'elasticita' di
sostituzione tra le risorse naturali e il lavoro-capitale composto sarebbe maggiore di uno. In questo caso, progresso
tecnologico a parte, il problema delle risorse non giustificherebbe previsioni catastrofiche.
Comunque altri autori hanno modificato le conclusioni di Solow utilizzando altre funzioni oppure introducendo altre
ipotesi sulla popolazione o sul progresso tecnico.
Stiglitz (42) ha evidenziato che, in presenza di una risorsa esauribile essenziale e di crescita esponenziale della
popolazione, e' possibile mantenere un livello di consumo pro-capite costante se il rapporto tra il tasso di variazione
della produzione, dovuto al progresso tecnico, e il tasso di crescita della popolazione sia maggiore dell'elasticita'
della produzione rispetto alla risorsa esauribile.
Per quello che riguarda la dinamica della popolazione, si e' rilevato da piu' parti come, in un mondo di dimensioni
finite, non ha senso supporre che la popolazione possa crescere esponenzialmente.
In un modello con risorse esauribili quindi spesso si abbandona questa ipotesi, dove il saggio di crescita della
popolazione e' dato esogenamente, e si considera la popolazione costante o crescente secondo un tasso endogeno,
correlato ad alcune variabili economiche.(43)
In quest'ultima ottica si pongono gli studi di Cigno (44) nei quali si suppone che il tasso di crescita della popolazione
sia positivamente correlato al consumo pro-capite ed inversamente correlato al grado di industrializzazione.
Abbiamo gia' visto come, in tutte le analisi precedenti, l'incertezza giochi un ruolo determinante.
A parte quella sulle stime delle riserve, tutte le altre incertezze dipendono, in ultima analisi, dalle possibilita'
offerte dal progresso che puo', con nuove tecnologie:
1) diminuire a parita' di output, l'imput necessario di risorsa;
2) riciclare la risorsa;
3) sostituire la risorsa con un'altra.
In generale si puo' affermare che "se e' abbastanza generalmente accettato che la dipendenza di un sistema
economico da alcune risorse esauribili non necessariamente porta a conclusioni catastrofiche, questo e' solo per
la fiducia in un evento incerto, il progresso tecnico (...)" (45).
Nella maggior parte dei modelli di crescita neoclassici, pero', si suppone che il progresso tecnico sia esogeno,
non comporti costi e proceda con regolarita'.
In alcuni contributi piu' raffinati, come quello di Dasgupta e Heal (46), benche' si ipotizzi che, grazie al progresso
tecnico, si potra' sostituire la risorsa esauribile, la data in cui si potra' farlo e' considerata una variabile
casuale.
Altri modelli trattano il progresso tecnico come variabile endogena.
Kamien e Schwartz (47), per esempio, fanno dipendere la probabilita' di ottenere un progresso tecnico dalla quantita'
di mezzi stanziati per la ricerca; e'ovvio che questi mezzi vanno sottratti al consumo o all'investimento in capitale
produttivo.
Gli autori concludono la loro analisi rilevando come lo sviluppo di una nuova tecnologia apre sempre una nuova
era, allontanando scenari deprimenti di recessione imposta dalla scarsita' di risorse essenziali. Questa nuova
era puo' dover essere soppiantata da un'altra, quando ostacoli ambientali o di scarsita' delle risorse si presentino
nuovamente. Infatti, in primo luogo, diverse tecnologie possono comportare diversi costi o rischi e ci si puo'
chiedere quali sia meglio sviluppare. In secondo luogo lo sviluppo di una nuova tecnologia potrebbe richiedere
una quantita' di risorse al di sopra di un certo livello.
Questo fatto ci pone, secondo Kamien e Schwartz, un'impor-tante domanda: se lo sviluppo di una nuova tecnologia
non e' iniziato entro il suo tempo di partenza ottimale, potrebbe essere ulteriormente rimandato poiche' i suoi
costi, relativamente alle risorse decrescenti dell'eco-nomia, sono aumentati? Se questo puo' accadere, allora noi
potremmo affrontare la possibilita' di avviarne lo sviluppo troppo tardi, nel senso che sarebbe impossibile reperire
il minimo di risorse richieste.
Il vincolo esercitato sulla crescita economica potenziale da una risorsa esauribile puo' essere rallentato non
solo dalla scoperta di un sostituto, ma anche dalla pos-sibilita' di riciclaggio.
Poiche' le risorse utilizzate nei processi di produzione, se non vengono riciclate, spesso ritornano nell'ambiente
inquinando, questo processo andrebbe considerato anche in una prospettiva di conservazione ecologica.
Comunque nelle decisioni sulle politiche ottime di sfruttamento, nel caso che il riciclaggio sia gia' attuabile
con la presente tecnologia, si cerca di stabilire quando e in che entita' iniziarlo (48).
Va ricordato tuttavia che la possibilita' di riciclaggio non e' infinita, in quanto le leggi fisiche garantiscono
che, ad ogni modo, attraverso di esso non e' possibile riottenere l'intera quantita' iniziale (49).